What is a similarity transformation
What Is A Similarity Transformation. Change to a new basis (p), perform the simple transformation (s), and change back to the old basis (p −1). (c) suppose that all the eigenvalues of are integers and. Two figures are similar if there exists a similarity transformation that maps one figure onto the other. The simplest similarity transformation method for eigenvalue computation is the jacobi method which deals with the standard eigenproblem , i.e., the mass matrix is the identity matrix.
Similarity Transformations Rotation, Reflection, & Translation (Video) From tutors.com
When written explicitly in terms of transformation matrices in three dimensions, similarities are. The fixed amount of the change is called the scale factor. If a,b ∈ g where g is a group, then the composition ab ∈ g. A transformation of a euclidean space obtained from such transformations as translations, rotations, and those which either shrink or expand the length of vectors. Consider a similarity transformation defined by the following matrix. Similar figures have the same shape but they may have different sizes.
Let be an invertible matrix.
Two figures are similar if there exists a similarity transformation that maps one figure onto the other. Similar matrices represent the same linear operator under two different bases, with p being the change of basis matrix. Two figures are similar if there exists a similarity transformation that maps one figure onto the other. A similarity transformation is a conformal mapping whose transformation matrix can be written in the form. Engage ny�s files mathematics high school: Change to a new basis (p), perform the simple transformation (s), and change back to the old basis (p −1).
Source: youtube.com
The simplest similarity transformation method for eigenvalue computation is the jacobi method which deals with the standard eigenproblem , i.e., the mass matrix is the identity matrix. Engage ny�s files mathematics high school: Theorem 3 for any two circles, positioned outside of each other, there is a transformation of scaling that transforms one into the other. Similarity transformation definition, a mapping of a set by which each element in the set is mapped into a positive constant multiple of itself, the same constant being used for. Similar triangles have congruent angles, and the ratios of corresponding sides are.
Source: youtube.com
Theorem 1 scaling of a circle results in a circle. A group of transformation s that will preserve the angles between any two curves at their intersecting points. A transformation that preserves angles and changes all distances in the same ratio, called the ratio of magnification. Similar matrices represent the same linear operator under two different bases, with p being the change of basis matrix. Let be an complex matrix.
Source: tekportal.net
(b) if is odd and , then prove that is an eigenvalue of. A similarity transform is a special kind of affine transformation that preserves shape. The fixed amount of the change is called the scale factor. Engage ny�s files mathematics high school: Similar matrices represent the same linear operator under two different bases, with p being the change of basis matrix.
Source: pinterest.co.uk
Similarity transformation definition, a mapping of a set by which each element in the set is mapped into a positive constant multiple of itself, the same constant being used for. (b) if is odd and , then prove that is an eigenvalue of. If is odd and , then prove that is an eigenvalue of. Two figures are similar, if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. Consider a similarity transformation defined by the following matrix.
Source: tutors.com
In effect, the similarity transform operates in three steps: (b) if is odd and , then prove that is an eigenvalue of. Matrix similarity, for matrix transformations of. Theorem 2 any two circles are similar. A transformation that changes the distance between points by a fixed amount is called a similarity transformation or a dilation*.
Source: slideserve.com
The term similarity transformation is used either to refer to a geometric similarity, or to a matrix transformation that results in a similarity. You can think of this as some combination of (1) translation, (2) rotation, (3) uniform scaling (all dimensions are scaled the same way), and (4) reflection. Two figures are similar if there exists a similarity transformation that maps one figure onto the other. The simplest similarity transformation method for eigenvalue computation is the jacobi method which deals with the standard eigenproblem , i.e., the mass matrix is the identity matrix. If is odd and , then prove that is an eigenvalue of.
Source: youtube.com
Theorem 1 scaling of a circle results in a circle. Theorem 3 for any two circles, positioned outside of each other, there is a transformation of scaling that transforms one into the other. If is odd and , then prove that is an eigenvalue of. Theorem 1 scaling of a circle results in a circle. The fixed amount of the change is called the scale factor.
Source: youtube.com
What are similarity transformations, and why do we need them? A transformation of a euclidean space obtained from such transformations as translations, rotations, and those which either shrink or expand the length of vectors. The simplest similarity transformation method for eigenvalue computation is the jacobi method which deals with the standard eigenproblem , i.e., the mass matrix is the identity matrix. The radii of these circles are related by a scaling factor. If is odd and , then prove that is an eigenvalue of.
Source: slideserve.com
In effect, the similarity transform operates in three steps: If is odd and , then prove that is an eigenvalue of. Similarity is an equivalence relation on the space of square matrices. Similarity transformation may refer to: A transformation that changes the distance between points by a fixed amount is called a similarity transformation or a dilation*.
Source: tutors.com
A transformation that preserves angles and changes all distances in the same ratio, called the ratio of magnification. (b) if is odd and , then prove that is an eigenvalue of. Change to a new basis (p), perform the simple transformation (s), and change back to the old basis (p −1). Theorem 1 scaling of a circle results in a circle. The simplest similarity transformation method for eigenvalue computation is the jacobi method which deals with the standard eigenproblem , i.e., the mass matrix is the identity matrix.
Source: slideserve.com
What are similarity transformations, and why do we need them? The similarity, affine, and perspective transformations are group operators, which means that each family of transformations constitutes an equivalence class. Two figures are similar, if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. (a) if for some complex number , then prove that either or is a singular matrix. The radii of these circles are related by a scaling factor.
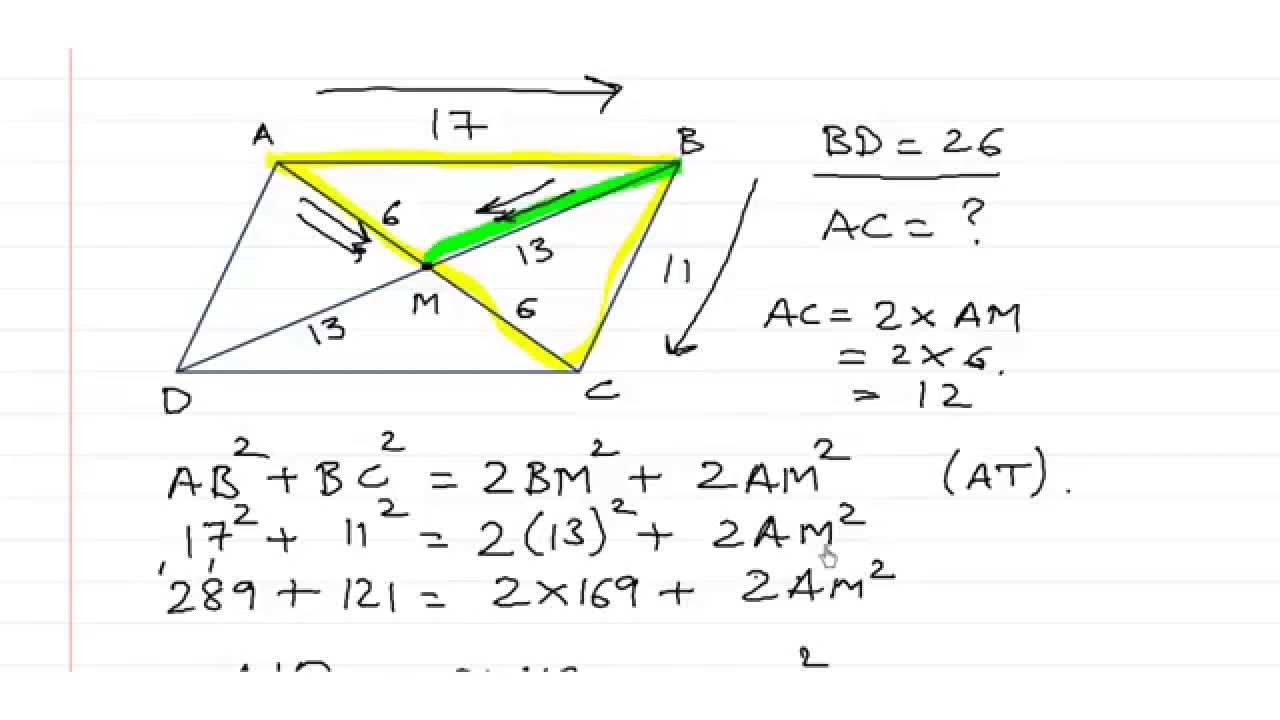
Source: youtube.com
Let be an complex matrix. In effect, the similarity transform operates in three steps: A transformation that changes the distance between points by a fixed amount is called a similarity transformation or a dilation*. Preserving shape means that a similarity transform also preserves angles (c) suppose that all the eigenvalues of are integers and.
Source: youtube.com
Engage ny�s files mathematics high school: (b) if is odd and , then prove that is an eigenvalue of. Try the free mathway calculator and problem solver below to practice various math topics. Let be an complex matrix. Consider a similarity transformation defined by the following matrix.
Source: youtube.com
Two figures are similar, if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. A similarity transformation takes one triangle and creates a similar triangle. (b) if is odd and , then prove that is an eigenvalue of. A similarity therefore transforms figures into similar figures. Theorem 1 scaling of a circle results in a circle.
Source: tutors.com
A transformation that preserves angles and changes all distances in the same ratio, called the ratio of magnification. Similarity transformation may refer to: Two figures are similar, if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. Two figures are similar if there exists a similarity transformation that maps one figure onto the other. A similarity transform is a special kind of affine transformation that preserves shape.
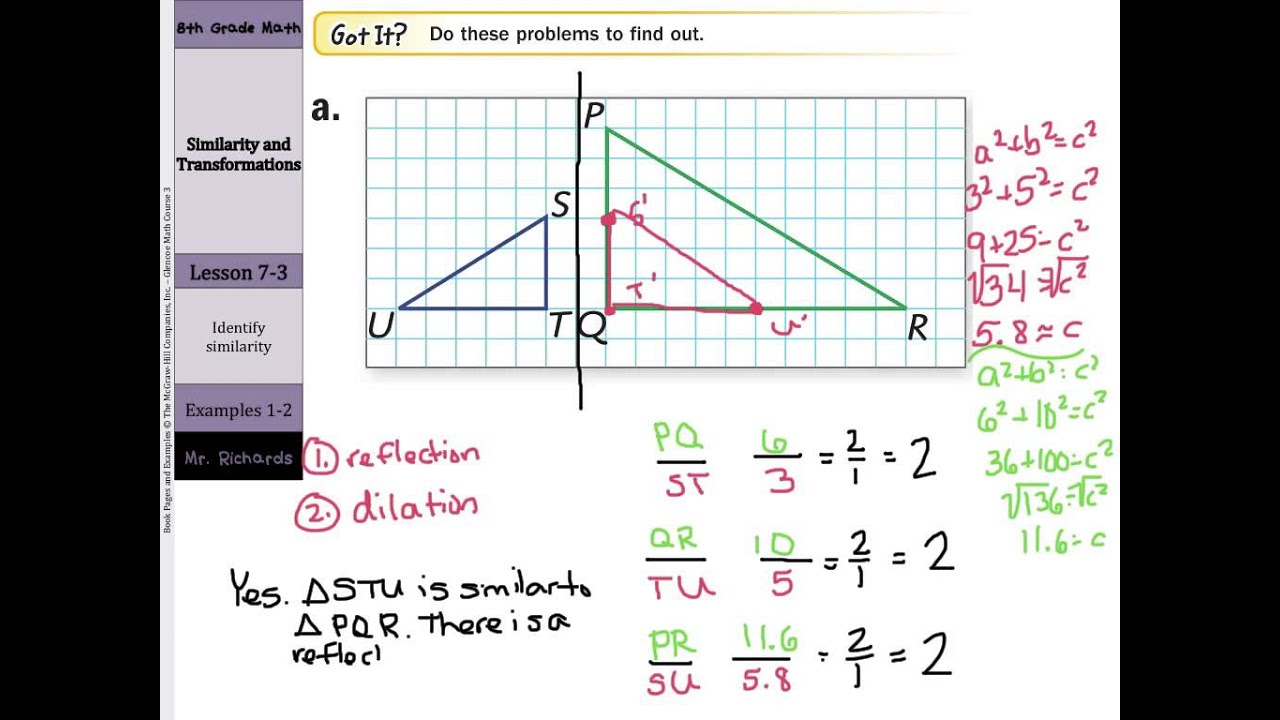
Source: media4math.com
If two figures are similar, there must be a sequence of translations, reflections, rotations, and/or dilations that can transform one to the other. Let be an complex matrix. A transformation of a euclidean space obtained from such transformations as translations, rotations, and those which either shrink or expand the length of vectors. Theorem 2 any two circles are similar. The fixed amount of the change is called the scale factor.
Source: slideserve.com
Try the given examples, or type in your own problem and. A similarity therefore transforms figures into similar figures. Two figures are similar, if one can be obtained from the other by a sequence of translations, reflections, rotations, and dilations. The fixed amount of the change is called the scale factor. If a,b ∈ g where g is a group, then the composition ab ∈ g.
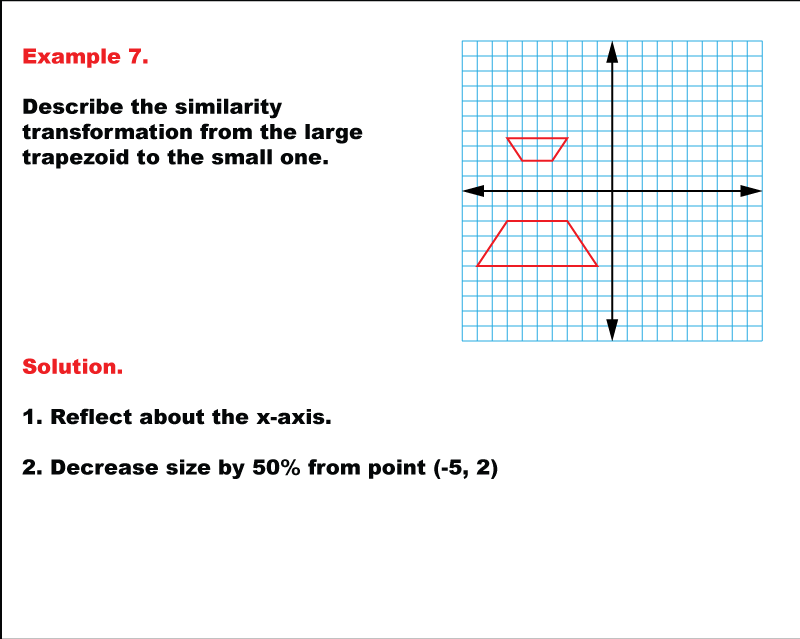
Source: youtube.com
Change to a new basis (p), perform the simple transformation (s), and change back to the old basis (p −1). If is odd and , then prove that is an eigenvalue of. A similarity can also be defined as a transformation that preserves ratios of distances. A similarity transform is a special kind of affine transformation that preserves shape. Similar triangles have congruent angles, and the ratios of corresponding sides are.
If you find this site helpful, please support us by sharing this posts to your own social media accounts like Facebook, Instagram and so on or you can also bookmark this blog page with the title what is a similarity transformation by using Ctrl + D for devices a laptop with a Windows operating system or Command + D for laptops with an Apple operating system. If you use a smartphone, you can also use the drawer menu of the browser you are using. Whether it’s a Windows, Mac, iOS or Android operating system, you will still be able to bookmark this website.
